Obelix erweitert seine Hinkelstein-Produktion
Obelix verfolgt eine neue Geschäftsidee. Er will seine Hinkelsteine ab sofort per Schiff transportieren. Der Schiffskapitän bietet ihm an seine Hinkelsteine zu transportieren, jedoch soll Obelix pro m^3 eine Goldmünze Transportkosten bezahlen. Obelix ist völlig überfordert. Wie soll er denn nun herausfinden, wie viel er zu zahlen hat? Kannst du ihm helfen?

Wenn man beide Augen zu drückt kann man das Volumen eines Hinkelsteines aus dem zweier Kegel zusammensetzen. Obelix sagt dass der obere Teil seiner Steine immer 5/7 der gesamten Höhe ausmachen, während der untere Teil nur 2/7 ausmacht. Die Höhe variiert jedoch von Stein zu stein. Der Radius an der dicksten Stelle Beträgt jedoch immer 1/10 der Höhe.

Somit kann das Volumen eines Hinkelsteins wie folgt berechnet werden:
Volumen = 1/3 * PI * (1/10 * Höhe) ^ 2 * 5/7 * Höhe + 1/3 * PI * (1/10 * Höhe) ^ 2 * 2/7 * Höhe
Spitzfindige Leser merken vermutlich, dass sie bei dieser Formel noch einiges vereinfachen lässt, jedoch ist das nicht das worum wir uns kümmern wollen. Denn Obelix hat VIELE Hinkelsteine. Wenn wir das Volumen aller von Hand ausrechnen wollten würden wir Wochen brauchen, doch morgen soll die Fracht schon verschifft werden. Kann uns ein Computer helfen?
Berechnen wir zuerst einmal anhand einer Beispielhöhe das Volumen eines Hinkelsteins:

Ein Traum… Doch wie gesagt haben wir viele Hinkelsteine – was nun? Vielleich so? :
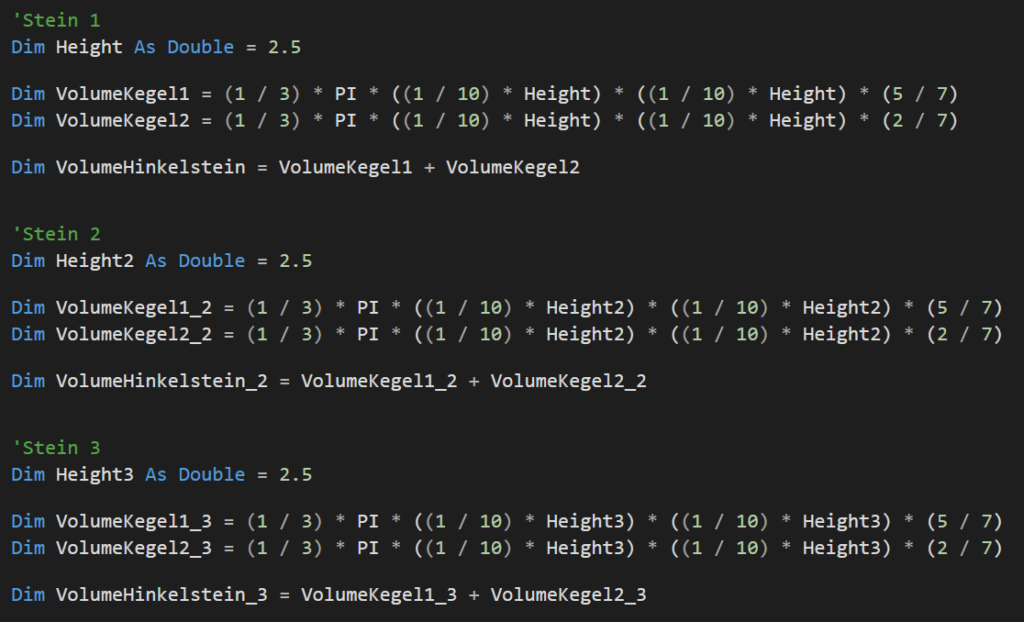
Funktionieren würde das vielleicht, jedoch hat dieser Ansatz die gleichen Zeilen immer wieder zu kopieren viele Nachteile.
Zum Einen ist es sehr viel „Schreibaufwand“ und beim kopieren können leicht Fehler entstehen. Und zum Anderen ist dieser Code schlecht lesbar – man versteht nur mit Mühe, was er tun soll. Dazu kommt noch, dass wenn sich etwas an unserer Formel für das Volumen ändert, müssen wir alle Vorkommnisse suchen, alle ändern und hoffen, dass wir keins verpassen.
Doch was sollten wir stattdessen tun? Wenn sich eine Funktionalität immer wieder wiederholt ist es sinnvoll und wichtig diese in eine Funktion auszulager. Mit der Zeit bekommt man ein Auge dafür, und es passiert größtenteils automatisch.
Doch was ist eine Funktion überhaupt? Eine Funktion ist eine Abfolge von Befehlen, die ich aufrufen kann um eine Aufgabe zu erledigen. Stell sie dir vielleicht wie ein Arbeiter vor. Eine Person, die super gut eine bestimmte Aufgabe erledigen kann (wie das Volumen eines Hinkelsteins berechnen). Solltest du ihre Dienste benötigen, dann sagst du dieser Person einfach, dass sie dir helfen soll und sie wird es tun.
Jedoch kann es sein, dass diese noch ein paar Dinge von dir braucht. Beispielsweise müssen wir in unserem Fall dieser Person sagen, wie groß der Hinkelstein ist, da sie sonst die Formel nicht anwenden kann. Doch wenn wir ihr die Höhe geben, kann sie uns das Volumen zurückgeben, sobald sie fertig ist.
Eine weitere tolle Eigenschaft von Funktionen ist, dass du nicht wissen musst, wie sie funktionieren um sie zu verwenden. Wie du auch nicht backen können musst und trotzdem den Bäcker um einen Kuchen bitten kannst, kannst du Funktionen aufrufen, ohne zu wissen, wie sie das gewünschte Verhalten ausführen.
Aber jetzt konkret… Wie sieht denn die Funktion für unsere Hinkelsteine aus?
Unsere Funktion bekommt als Eingabe die Höhe eines Hinkelsteins und soll uns als Ausgabe das Volumen zurückgeben. Im Code sieht das wie folgt aus:

Um eine Funktion zu erstellen schreibt man zuerst das Wort „Function“. Darauf folgt der Funktionsname (im Bild in orange). Das ist der Name unter dem du nachher die Funktion aufrufen kannst. Darauf folgt in einer Klammer eine Liste von Eingabeparametern (in blau). In diesem Fall brauchen wir jedoch nur einen. Um die erste Zeile abzuschließen folgt dann doch der Rückgabeparameter (in grün).
Anschließend folgen die Befehle die die Funktion ausführen soll (in lila) und ein „End Function“. Die Befehle die Ausgeführt werden sollen nennt man auch den Methodenrumpf. Methode ist dabei ein anderes Wort für Funktion. Der Methodenrumpf beschreibt das Verhalten der Funktion und kann ausschließlich auf die Eingabeparameter oder Variablen, die im Rumpf selbst deklariert wurden zugreifen. In diesem Fall kann also nur auf „Height“, „VolumeKegel1“, „VolumeKegel2“ und „VolumeHinkelstein“ zugegriffen werden. Das kann man sich auch wieder mir der Person veranschaulichen, die die Arbeit für die erledigt. Stell dir vor sie wohnt in einer anderen Stadt. Wenn du nun von ihr das Volumen eines Hinkelsteins ausrechnen lassen willst, dann schickst du einen Auftrag. In diesem MUSS die Höhe des Steins stehen, da der Arbeiter sonst nicht arbeiten kann. Dieser kann jedoch bei sich zuhause neue Zwischenergebnisse, wie „VolumeKegel1“, „VolumeKegel2“ und „VolumeHinkelstein“ erstellen. Diese wirst du jedoch nie zu Gesicht bekommen. Du bekommst nur das Ergebnis zurück. Nämlich eine einzige Zahl – das Volumen.
Nachdem die Funktion nun deklariert wurde (wir wie oben gesagt haben, wie sie aussieht), können wir sie nun verwenden. Dazu müssen wir nur den Namen der Funktion gefolgt von einer Klammer in der die Eingabeparameter stehen schreiben.
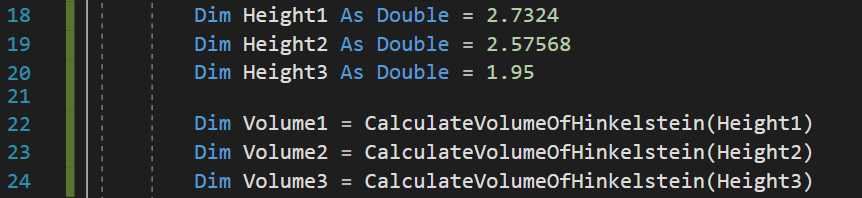
Wenn wir uns beispielsweise Zeile 22 anschauen, sehen wir, wie die Funktion aufgerufen wird. Wir wollen das Ergebnis der Berechnung in die Variable Volume1 schreiben. Der Eingabeparameter der Funktion ist „Height1“. Das heißt der Wert von Height1 wird kopiert und in die Funktion eingesetzt. Dort hat also „Height“ den gleichen Wert. Jedoch würden sich Änderungen von „Height“ nicht auf „Height1“ auswirken.
Nun können wir uns viel Schreibarbeit sparen und gleichzeitig viel einfacher verstehen, das der Code tut. Da der Name „CalculateVolumeOfHinkelstein“ uns schon sehr viele Informationen gibt.
Quizzzzz time
Frage 1: Welche Eingabeparamter braucht eine Funktion, die den Umfang eines Kreises ausrechnet?
Eine solche Funktion braucht lediglich den Radius oder den Durchmesser des Kreises. Dann kann durch die Formel 2 * PI * Radius oder PI * Durchmesser der Umfang berechnet werden.
Frage 2: Welchen Rückgabetyp hatte eine Funktion, die einen Kreisumfang ausrechnet?
Sie hätte normalerweise den Typ Double oder Single – Also eine Kommazahl.
Aufgabe 3: Schreibe eine solche Funktionsdefinition auf und außerdem, wie sie mit einem Radius von 5 aufgerufen werden kann.
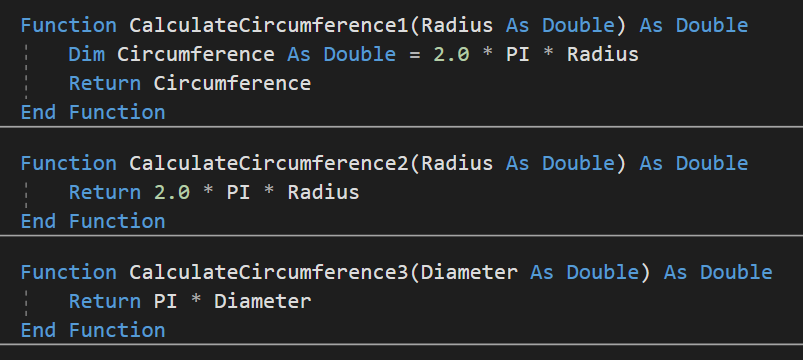
Hier sind drei Beispiele, wie eine solche Funktion aussehen könnte. Versuche herauszufinden, was die Unterschiede sind und warum sie trotzdem das Selbe tun.
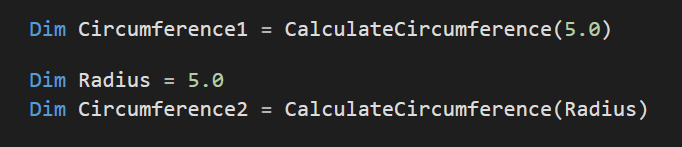
Und hier sind zwei Möglichkeiten, wie ich diese Funktion aufrufen kann. Entweder der Wert kann direkt eingegeben werden oder man kann eine Variable als Eingabe verwenden.
Herzlichen Glückwunsch! Du hast ein weiteres wichtiges Puzzlestück der Programmierung kennen gelernt. Beim nächsten Mal kann es richtig los gehen…

